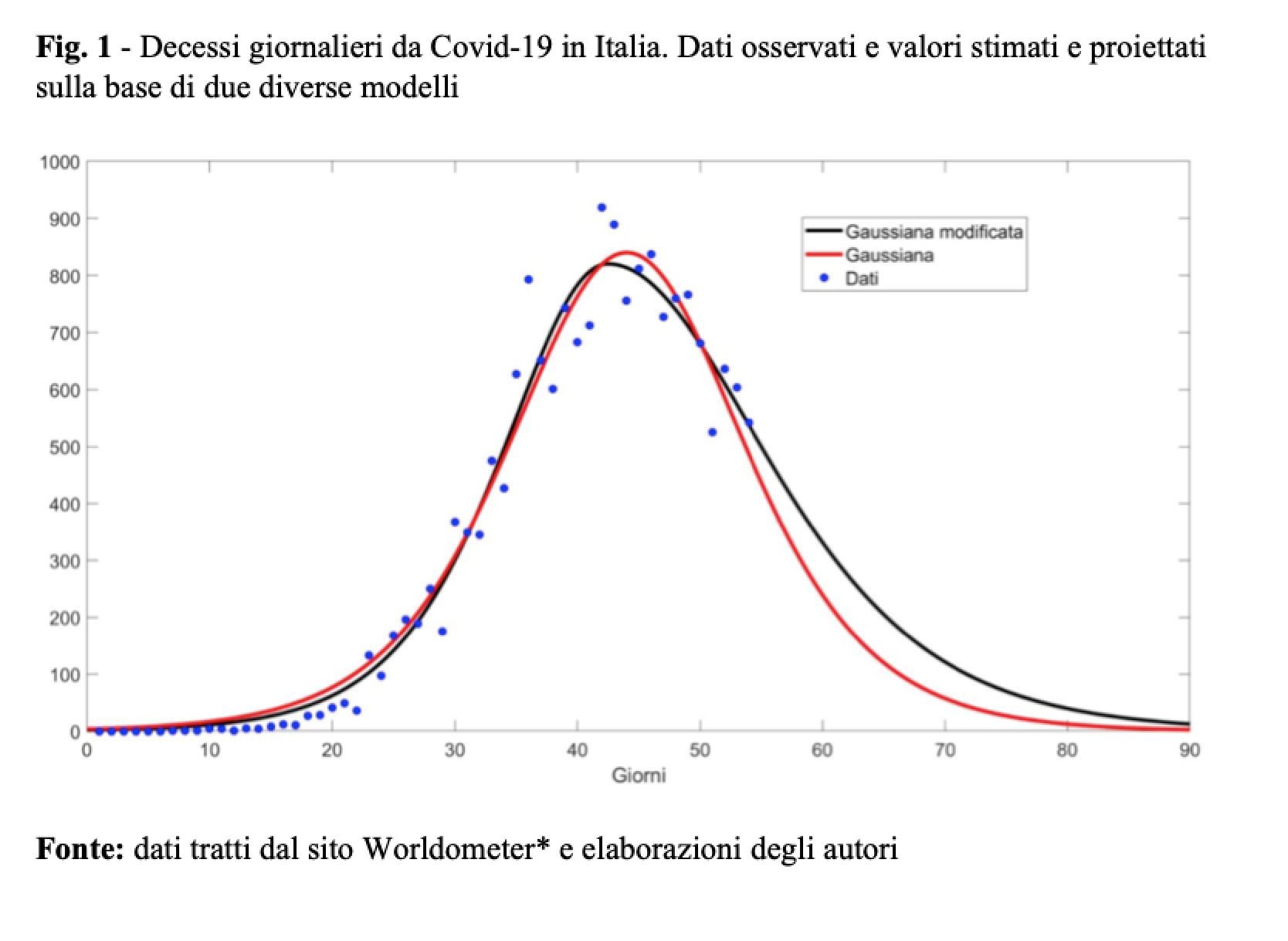
Fino a ieri, 8 aprile, abbiamo proposto ai lettori di Neodemos curve modello potenzialmente in grado di descrivere l’evoluzione della pandemia da Covid-19, con riferimento sia al numero di casi giorno per giorno (curva normale, o gaussiana; fig. 1, linea rossa), sia al totale (cumulato) di questi casi (curva logistica, fig. 2, linea rossa). Lo abbiamo fatto sia per gli infetti sia per i decessi, ottenendo quindi quattro curve, ma per ragioni di semplicità ci riferiremo adesso solo ai decessi.
Sempre per ragioni di semplicità, riferiamoci solo alla figura 1 (la curva a campana) visto che da questa è poi possibile ricavare anche l’altra (o viceversa, ma non stiamo ora a complicare).
Ebbene, la curva modello che abbiamo usato per approssimare i punti funziona bene, anche da un punto di vista teorico, in condizioni… teoriche, appunto, che però non sempre rispecchiamo la realtà.
Un territorio non omogeneo
Ad esempio, non è vero che tutti hanno la stessa probabilità di entrare in contatto con tutti gli altri, e quindi eventualmente di infettarli: chi sta a Milano, raramente vede un palermitano o un triestino. Vi è insomma una suddivisione del territorio in sotto aree, relativamente chiuse all’esterno ma aperte all’interno, ognuna delle quali presumibilmente caratterizzata dalla sua specifica curva “normale” (v. Mauro Maltagliati su Neodemos ). A livello nazionale, l’epidemia, pur se ben descritta da varie curve dello stesso tipo, non riproduce la curva della figura 1 (linea rossa). Ma di questo limite non tratteremo qui, anche per la difficoltà di capire in quali e quante sotto aree sarebbe opportuno suddividere il territorio nazionale.
L’azione di contrasto dell’uomo
Un’altra ragione di allontanamento della realtà dalla teoria sta nell’azione dell’uomo. Come già illustrato, per esempio, da Massimo Livi Bacci su questo sito la forma della curva della figura 1 cambia, pur restando della stessa “famiglia”, a seconda che vi sia o meno intervento da parte delle autorità sanitarie, ad esempio con l’imposizione del distanziamento sociale: senza intervento si ha la curva in viola della fig. 3 (maggior numero e maggior concentrazione di casi), mentre con intervento si ha la curva azzurrina (le cose vanno meglio, ma la pandemia dura più a lungo).
Ma che succede se l’intervento dell’uomo cambia durante il processo, e cioè se il distanziamento sociale viene imposto solo in ritardo rispetto allo scoppio dell’epidemia? In questo caso il risultato sarà un ibrido delle due curve: inizialmente la salita è ripida (come nella curva viola), ma poi la discesa è più lenta (come nella curva azzurrina). Il picco verrà più o meno abbassato a seconda di quanto tempestivo e efficace è stato l’intervento dell’uomo.
Ebbene, la curva nera della figura 1 fa proprio questo: parte da una curva standard (normale, o gaussiana), e ne modifica la parte destra, “rompendone” la simmetria e permettendole di scendere a una velocità (meglio: con una pendenza) diversa da quella con cui è salita. A stime fatte, questa pendenza si rivela in effetti minore, come era da attendersi, grazie all’intervento delle autorità e ai comportamenti delle persone. Poiché questa nuova famiglia di curve, un po’ più complicata ma più realistica, si adatta meglio alla realtà, da oggi, 9 aprile Neodemos propone le sue stime e le sue previsioni su questa base.
Si, ma…?
Vi chiederete che cosa cambia in pratica. Le cose peggiorano un poco, sia in termini di numero totale di eventi (la proiezione dei morti totali, ad esempio, passa da circa 20 mila a circa 25 mila) sia in termini di data di “fine”, che passa dal 25 aprile a 18/19 maggio.
(NB. Entrambe le stime sono state fatte oggi, 9 aprile, e presumibilmente cambieranno nel tempo. A questo proposito ricordiamo anche che la “fine” è qui convenzionalmente definita come il giorno passato il quale si registrerà solo un ridotto numero di eventi, che abbiamo arbitrariamente fissato all’1%. Nel caso dei decessi, ad esempio, se fosse corretta la proiezione di 25 mila decessi totali, dopo il giorno che noi dichiariamo di “fine” si produrrebbero però ancora 250 decessi.) Ma ci sono anche buone notizie: le proiezioni precedenti, più ottimistiche, peggioravano però di giorno in giorno (proprio per il fatto che la curva modello sottostante non era la più adatta al caso) mentre le proiezioni attuali, più pessimistiche, tendono invece a migliorare man mano che si aggiungono nuovi dati (o almeno questo è quello che abbiamo verificato fino a questo momento). Il perché ciò avvenga è in parte spiegato qui sotto.
Vi potreste infatti anche chiederete perché non abbiamo adottato fin da subito il nuovo modello, se lo pensavamo migliore. La risposta è che il nuovo modello richiede informazioni sul tratto discendente della curva per poterne stimare la pendenza, che si immagina (e in effetti risulta) diversa dalla pendenza “in salita”, misurata sul ramo sinistro. Avevamo quindi bisogno di dati successivi al picco. Ora li abbiamo, ma sono ancora relativamente pochi, ed è (anche) per questo che la nuova curva stimata continua ad adattarsi man mano che arrivano nuovi dati. Sulla base delle valutazioni degli ultimi giorni, tuttavia, stime e proiezioni cominciano ad apparire relativamente stabili.
Fonte figure
*Fonte: dati tratti dal sito worldometers.info